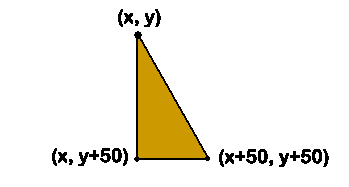
Modify your previous program so that each of your 500 random triangles is the same size and shape. Choose a random color as before. Then choose a single x and y value for one vertex. Then, you must compute the positions of the other two vertices. For a right triangle (which is easiest), if the upper-left vertex is at (x,y), then the lower-left vertex will be at (x,y+50) and the lower-right vertex will be at (x+50,y+50). See the diagram below.
|
If you don't choose your first point correctly, then part of the triangle won't fit on the screen. Make sure you choose small enough x- and y-values to make sure that all of the triangle is showing.
Here is a working example version:
For some extra credit, make all your triangles isosceles triangles rather than right triangles. Even better, make them equilateral triangles.
For maximum extra credit, do one of two things: make all your triangles equilateral, but make their sizes vary. Alternatively, make the triangles by randomly choosing one vertex and then two of the side lengths within some reasonable range and then computing what the length of the third side should be and the locations of the vertices in order to draw the triangle.
©2013–2015 Graham Mitchell
This assignment is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 United States License.
![]()